GLOSSARIO: Odds Ratio
L'odds ratio è una misura statistica utilizzata per quantificare l'associazione tra un'esposizione e un esito. [Lettura 6 min]
L'odds ratio (OR) è una misura statistica ampiamente utilizzata in epidemiologia e ricerca clinica per quantificare l'associazione tra un'esposizione e un esito.
In particolare, l'OR è spesso impiegato negli studi caso-controllo per confrontare le probabilità di un determinato evento tra due gruppi.
L'OR fornisce una misura più precisa e interpretabile della forza dell'associazione rispetto al semplice confronto delle percentuali tra i due gruppi.
La maggiore utilità di questo parametro si ha quando le dimensioni dei gruppi sono disomogenee o quando la prevalenza dell'evento è bassa.
Calcolo dell'Odds Ratio
L'OR si calcola come rapporto tra le probabilità che l'evento si verifichi nei due gruppi.
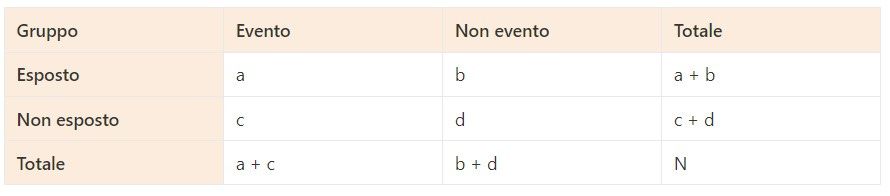
Si costruisce una tabella di contingenza 2x2 come quella qui sotto:
OR = (a / (a + b)) / (c / (c + d))dove:
a è il numero di casi con l'evento nel gruppo esposto
b è il numero di casi senza l'evento nel gruppo esposto
c è il numero di casi con l'evento nel gruppo non esposto
d è il numero di casi senza l'evento nel gruppo non esposto
Interpretazione dell'Odds Ratio:
OR = 1: non c'è associazione tra il fattore di rischio e l'evento.
OR > 1: il fattore di rischio aumenta la probabilità dell'evento.
OR < 1: il fattore di rischio riduce la probabilità dell'evento.
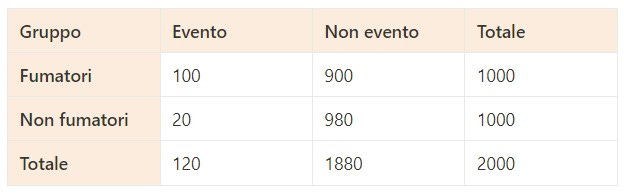
Esempio: supponiamo di voler studiare l'associazione tra fumo e cancro ai polmoni. In uno studio, si osserva che su 1000 fumatori, 100 sviluppano il cancro ai polmoni, mentre su 1000 non fumatori, solo 20 sviluppano la malattia.
La tabella di contingenza in questo caso è:
OR = (100 / 900) / (20 / 980) = 5
Questo significa che i fumatori hanno una probabilità 5 volte maggiore di sviluppare il cancro del polmone rispetto ai non fumatori.
Limiti dell'Odds Ratio
Mancanza di informazioni sulla grandezza dell'effetto: l'OR indica solo la direzione e la forza relativa dell'associazione, ma non fornisce informazioni sulla grandezza dell'effetto.
Esempio: un OR di 2 potrebbe indicare un piccolo aumento del rischio o un grande aumento del rischio, a seconda della prevalenza dell'evento nella popolazione.
Influenza della dimensione del campione: un campione di piccole dimensioni può produrre un OR fuorviante; l'OR è più affidabile quando il campione è grande e rappresentativo della popolazione.
Influenza di altri fattori di rischio: l'OR non tiene conto di altri fattori di rischio che potrebbero influenzare l'evento.
Esempio: l'OR per l'associazione tra fumo e cancro del polmone può essere influenzato da altri fattori di rischio come l'esposizione all'amianto o la predisposizione genetica.
Difficoltà nell'interpretazione con valori estremi: quando uno dei valori di a, b, c o d è molto piccolo o molto grande, l'OR può essere difficile da interpretare. In questi casi è preferibile utilizzare altre misure di associazione, come il rischio relativo o la differenza di rischio.
Non implica causalità: l'OR indica solo un'associazione, non una causalità. È possibile che altre variabili non misurate siano responsabili dell'associazione osservata.
Difficoltà nella generalizzazione: l'OR calcolato in un campione specifico potrebbe non essere generalizzabile ad altre popolazioni.
Odds Ratio e Rischio Relativo
Sia l’OR sia il rischio relativo (RR) quantificano la forza dell'associazione tra un'esposizione e un outcome.
L'OR è una misura della probabilità di un evento rispetto alla probabilità che l'evento non si verifichi, mentre l’RR è una misura diretta del rischio di un evento in un gruppo rispetto a un altro gruppo.
Nonostante l'OR possa essere meno intuitivo e talvolta meno preciso dell’RR, ci sono situazioni specifiche in cui è necessario l'uso dell'OR, come negli studi caso-controllo, dove non è possibile calcolare direttamente il rischio assoluto: l'OR è l'unica misura disponibile per stimare l'associazione tra esposizione ed esito.
Quando l'evento è raro (indicativamente con una frequenza <10%), l'OR approssima bene l’RR e i due valori sono intercambiabili: in questo caso l'OR può essere interpretato come RR in modo abbastanza affidabile.

Al contrario, quando l'evento è frequente (indicativamente >15-20%), l'OR tende a sovrastimare il RR e l'approssimazione non è più valida.
Quando l’RR esprime l’efficacia di un trattamento, con eventi frequenti l’OR tende a sovrastimare l’efficacia: anche per questa ragione, esiste un consenso pressoché unanime sulla non opportunità di utilizzare l’OR per esprimere l’efficacia dei trattamenti.
Esempio: supponiamo di voler valutare se l'uso di aspirina a basse dosi riduce il rischio di infarto miocardico (IM) nei pazienti con malattia coronarica stabile, rispetto al placebo.
In questa popolazione l'incidenza annuale di IM è relativamente bassa (<5%), l'OR stimato confrontando il gruppo trattato con aspirina vs placebo sarà numericamente molto simile all’RR: in questo caso l'OR potrà essere interpretato come RR in modo abbastanza affidabile.
Volendo studiare l'effetto dell'aspirina su un outcome più frequente, come il sanguinamento gastrointestinale (incidenza >10%), allora l'OR tenderebbe a sovrastimare l’RR.
In questo secondo caso, l'approssimazione OR ≈ RR non sarebbe più accettabile e bisognerebbe considerare l’RR per evitare di sopravvalutare il rischio emorragico associato all'aspirina.
In pratica - L'odds ratio è uno strumento statistico per valutare l'associazione tra due variabili.
OR e RR misurano entrambi la forza di un'associazione, ma mentre l’RR è di facile interpretazione, l'OR approssima l’RR solo per eventi rari.
Nella pratica clinica è essenziale conoscere questa distinzione per interpretare correttamente i risultati degli studi e prendere decisioni terapeutiche razionali, bilanciando benefici e rischi dei trattamenti proposti.
Misure di associazione basate sulla differenza relativa del rischio: rischio relativo e odds ratio
G Tec Nefrol Dial 2017; 29 (4): 278-280
Misura del rischio: odds ratio e rischio relativo
Quaderni di epidemiologia
RRR, RR, OR, ARR, NNT: che confusione!
GIMBEnews - Vol. 2, n. 8 Novembre - Dicembre 2009